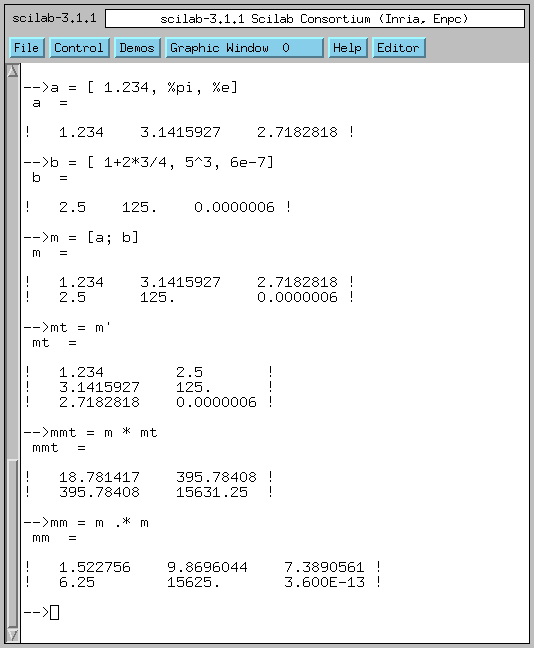
Après avoir lancé Scilab, on utilisera le logiciel d'abord
comme une calculatrice scientifique, matricielle et graphique,
en écrivant les commandes directement dans sa fenêtre de base ;
puis on s'en servira comme un langage informatique en écrivant le
code d'un programme dans son éditeur de texte avant de l'exécuter.
-->
prompt) puis les valider avec la touche <Return/Enter>
du clavier.
<↑> (flèche-haut) et
<↓> (flèche-bas) et, éventuellement, les modifier.

Les principaux objets manipulés dans Scilab sont les vecteurs et
les matrices : un vecteur est une matrice ligne ou
une matrice colonne, un scalaire est une matrice 1x1.
Les éléments d'une matrice sont encadrés par des crochets
droits [ et ], ceux d'une même ligne sont
séparés par une virgule (,)
(ou par des espaces, ce qui peut provoquer des confusions...).
Les quelques constantes usuelles sont précédées du symbole %
--> a = [ 1.234, %pi, %e]
Les opérations +, -, *, / sont habituelles,
^ est l'élévation à la puissance et la notation scientifique
est supportée
--> b = [ 1+2*3/4, 5^3, 6e-7]
Oups ! ne pas mettre d'espaces entre 1 et +2*3/4,
(il y a quelques gags surprenants dans Scilab).
Dans une matrice, les lignes sont séparées par un point-virgule
(;)
--> m = [ a; b]
La transposition s'obtient par une apostrophe (')
--> mt = m'
Les opérations + et - agissent, comme on s'y attend,
sur les matrices termes à termes qui doivent être de même taille.
Mais, attention, l'opérateur * est celui de la
multiplication matricielle ; pour la multiplication termes
à termes il faut utiliser .* (point et étoile,
sans espace entre).
Comparer
--> mmt = m * mt
et
--> mm = m .* m
La division termes à termes de matrices s'obtient par l'opérateur
./ (point et /, sans espace entre),
à ne, surtout, pas confondre avec / (sans point devant)
qui est la division matricielle : multiplication par la matrice
pseudo-inverse, ce qui peut donner des résultats inattendus...
Progressions arithmétiques
Les progressions arithmétiques s'obtiennent, comme vecteurs lignes,
avec la syntaxe debut:raison:fin
--> pa1 = 1:2:12
--> pa2 = 6:-1:1
Lorsque la raison est absente elle prend, par défaut,
la valeur 1
--> pa3 = 1:6
Il y a aussi linspace
--> help linspace
--> pa4 = linspace(0, 1, 11)
Les deux premiers arguments 0 et 1 sont les extrémités
et le dernier 11 est le nombre de piquets, la raison de la
progression vaut (1-0)/(11-1) car, c'est connu depuis l'école
primaire, il y a un intervalle de moins que de piquets.
Construction de matrices
--> id4 = eye(4,4)
--> nulles = zeros(3,2), uns = ones(2,3), quatres = 4*uns,
neufs = 5 + quatres
Plusieurs instructions sur une même ligne de commande doivent être
séparées soit par une virgule (,)
soit par un point-virgule (;) si on ne veut pas afficher
le résultat.
Enfin, remarquer que le 5 s'est adapté, tout naturellement,
à la taille de la matrice quatres.
[0,1], par défaut)
--> aleas = rand(3,4)
Attention au comportement de ces fonctions lorsqu'on les appelle avec un seul argument, celui-ci ne sert qu'à fournir le nombre de lignes et le nombre de colonnes du résultat, sa valeur exacte n'a aucune importance !
--> un = ones(1000), uns2 = ones(nulles), nulles2 = zeros(uns), aleas2 = rand(nulles)
Les matrices obtenues sont de même taille que l'unique argument :
dans le premier cas 1000 est interprété comme une matrice
1x1, dans le second on signale que l'on veut une matrice de
même dimension que nulles c'est-à-dire 3x2, etc.
Ce mécanisme est bien commode, mais est un peu vicieux!
À ce propos, pour obtenir dimension et taille de matrice, utiliser
les fonctions size ou length
--> size(1000), length(1000), size(nulles), length(nulles)
la fonction size renvoie un vecteur ligne
[nb_lignes,nb_colonnes]
tandis que la fonction length renvoie un (seul) entier :
le produit nb_lignes * nb_colonnes.
Remarquer que, lorsqu'une expression n'est pas affectée à une
variable, sa valeur est attribuée, par défaut, à ans
(answer).
Accès aux termes d'une matrice
La matrice m a été créée au début, pour la revoir
(disp : display, afficher)
--> disp(m)
Il faut utiliser des parenthèses ( , ) pour
accéder aux termes d'une matrice en donnant d'abord le numéro de
ligne (depuis 1) puis, séparé par une virgule
(,), le numéro de colonne (depuis 1)
--> m11 = m(1,1), m23 = m(2,3)
Attention à cela, les indices en Scilab
commencent à 1 et non pas
à 0 ; c'est agaçant, il faut faire avec !
Le message d'erreur invalid index
signale souvent qu'un indice vaut 0, ce qui est interdit.
On peut aussi donner une tranche d'indice (un vecteur d'entiers) dans
ce cas $ (dollar) représente le dernier indice, de ligne ou
de colonne suivant le cas,
--> m(2,2:3), m(2,2:$)
Un : (deux-points tout-nu) représente la totalité des
indices de ligne ou de colonne (équivalent donc à 1:$)
--> m(:,3), m(2,:)
ainsi m(:,3) est la colonne 3 de la matrice m et
m(2,:) sa ligne 2.
L'accès peut aussi se faire en écriture
--> m(:,3) = 1000
On peut supprimer un bloc de matrice en l'égalant à la matrice vide
--> m(:,3) = []
Attention, il y a un piège (il y en a de vicieux dans Scilab !),
si il est commode dans le cas de vecteur (c.-à-d. matrice
ligne ou matrice colonne) d'accéder aux termes avec un seul
indice (l'autre valant nécessairement 1) on peut aussi le faire
pour une matrice quelconque
--> m, m11 = m(1), m21 = m(2), m12 = m(3), m22 = m(4)
la numérotation s'effectuant colonnes par colonnes de haut en bas (puis de gauche à droite) ; en particulier,
--> tout = m(:)
pour transformer une matrice en vecteur colonne.
Fonctions agissant sur des matrices
On refabrique la matrice m initiale
--> m = [ a; b]
La plupart des fonctions mathématiques de Scilab
(log, exp, cos, tan, atan....)
agissent, naturellement, termes à termes, sur les matrices
--> sm = sqrt(m), lm = log(m), slm = sin(lm)
D'autres
(max, min, sum, mean, prod,...)
agissent sur l'ensemble des termes, ou sur les colonnes 'c',
ou sur les lignes 'r' (rows)
--> max(slm), max(slm, 'c'), max(slm, 'r')
--> disp(m), sum(m), sum(m, 'c'), sum(m, 'r')
Il n'est pas toujours facile de se rappeler quand utiliser 'c' ou
'r', faire un essai sur un cas simple
--> uns = ones(2,3), sum(uns), sum(uns, 'c'), sum(uns, 'r')
Les sommes et produits partiels (ou cumulés)
--> dix = 1:10, sommes = cumsum(dix), factoriels = cumprod(dix)
peuvent aussi utiliser ces arguments 'c' et 'r'
--> uns = ones(2,3), cumsum(uns), cumsum(uns, 'c'), cumsum(uns, 'r')
Les fonctions max et min peuvent avoir plusieurs arguments
de même dimensions (mais les scalaires s'adaptent naturellement
à la taille commune)
--> disp(m), slm6 = 6*slm, max(m, slm6, 3)
Les booléens
Les booléens ont seulement deux valeurs
T (vrai/true) ou
F (faux/false),
< et > pour les inégalités strictes ;
<= et >= pour les inégalités larges ;
== pour l'égalité ;
~= ou <> pour l'inégalité .
~ pour la négation (à placer devant l'opérande) ;
& pour le ET (à placer entre les opérandes) ;
| pour le OU (à placer entre les opérandes).
Attention, ne pas écrire && et || comme en Java ou en C/C++.
De plus, l'utilisateur devra noter les constantes vrai et
faux, respectivement, %T et %F
(les minuscules %t et %f sont aussi acceptées)
--> vrai = %t, faux = %F
La fonction double permet de transformer les booléens en scalaires
(1 pour %T et 0 pour %F)
--> v = double(vrai), f = double(faux)
cette conversion est souvent (mais pas toujours ???, se méfier !) implicite dans les expressions numériques
--> v = %T + 0, f = 1*%f
Accès aux termes d'une matrice par des vecteurs de booléens
On peut, aussi, accéder aux termes d'une matrice en donnant à la place
des indices de ligne et/ou de colonne un vecteur de booléens, alors seuls
les termes correspondant aux T (vrai/true) sont concernés.
Méditer ces quelques lignes
--> A = rand(1,6)
A =
0.2848294 0.8053452 0.7453589 0.2674080 0.4584525 0.8958010
--> A > 0.5
ans =
F T T F F T
--> B = A( A > 0.5 )
B =
0.8053452 0.7453589 0.8958010
--> A( A > 0.5 ) = 1000
A =
0.2848294 1000. 1000. 0.2674080 0.4584525 1000.
[] :
--> C = rand(1,6)
C =
0.9354626 0.0433594 0.5545320 0.5687664 0.2269803 0.2624333
--> C < 0.5
ans =
F T F F T T
--> C( C < 0.5 ) = []
C =
0.9354626 0.5545320 0.5687664
Les chaînes de caractères
Les chaînes de caractères sont encadrées par des guillemets simples
ou doubles
--> disp( 'Bonjour ' + "Toto" + string(5) )
elles se concatènent par l'opérateur + et on doit
convertir les expressions numériques par la fonction string( ).
plot2d(x, y, style),
et ses variantes, prennent, pour simplifier, essentiellement deux arguments :
le premier x est un vecteur (ou matrice) d'abscisses et le
second y un vecteur (ou matrice) d'ordonnées,
ils doivent être de dimensions compatibles.
Le troisième argument style est facultatif, ses valeurs peuvent être
0 les points de coordonnées x(i),y(i) sont
représentés par un pixel noir et ne sont pas reliés entre-eux
(contrairement aux valeurs suivantes) ;
1 le graphe est en noir, c'est la valeur par défaut ;
2 le graphe est en bleu ;
5 le graphe est en rouge ;
8 attention, le graphe est en blanc !
... la numérotation des couleur est plutôt farfelue...
plot2d sont
plot2d2 pour un graphe en escalier et
plot2d3 pour un graphe en bâtons.
clf.
--> clf, x = linspace(0, 5*%pi, 200); plot2d(x, sin(x))
Remarquer le point-virgule (;), on ne veut pas voir les
200 valeurs de x.
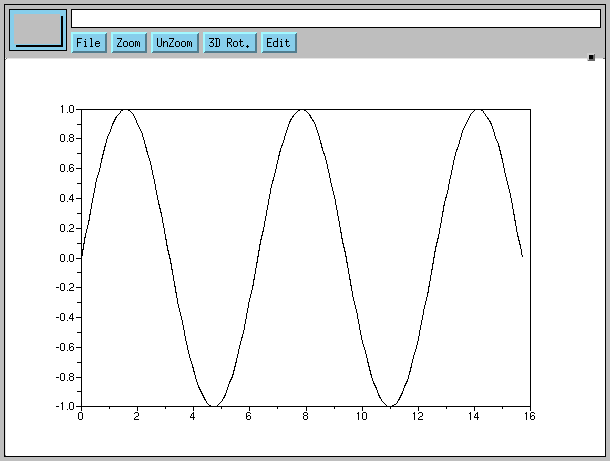
Un escalier en bleu
--> clf, x = linspace(0, 5*%pi, 20); plot2d2(x, sin(x), 2)
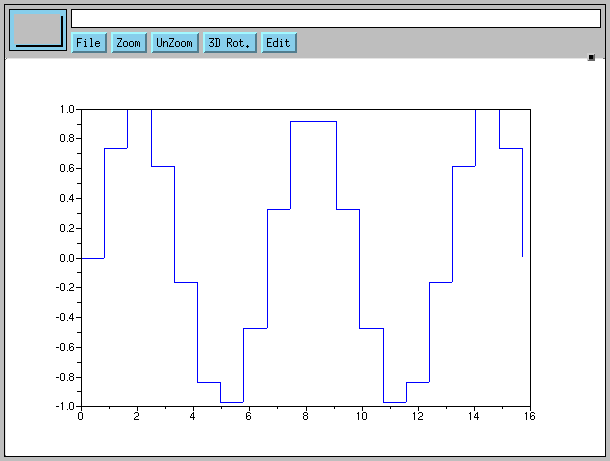
En bâtons rouges
--> clf, x = linspace(0, 5*%pi, 20); plot2d3(x, sin(x), 5)
rand().
À chaque appel
--> U = rand()
--> U = rand()
cette fonction fournit un "tirage au hasard" :
un nombre U, différent à chaque fois, sans aucun rapport
avec les précédents, compris entre 0 et 1 (strictement)
de telle manière que la probabilité de l'événement
{a < U < b} soit égale à b-a
(pour 0<a<b<1).
Autrement dit, la probabilité de tomber dans un sous-intervalle de
[0,1] est égale à la longueur de cet intervalle, qu'il soit
ouvert ou fermé. On parle, alors, de probabilité ou de loi uniforme
sur Ω = [0,1].
On peut aussi fabriquer des matrices dont tous les termes sont aléatoires
--> aleas = rand(3,5), aleas10 = rand(10,1), alea = rand(1000)
La dernière commande ne renvoie qu'une valeur, pourquoi ? On l'a dit quelque part plus haut !
Réalisation d'un événement
Pour simuler la réalisation (ou la non réalisation) d'un événement
de probabilité p il suffit de se fixer un intervalle A de
longueur p, contenu dans l'intervalle [0,1], et
d'observer si la valeur obtenue par l'appel de rand() tombe (ou ne
tombe pas) dedans.
Bien entendu, le plus naturel est de prendre pour A l'intervalle
[0,p] ou [1-p,1], ouvert ou fermé, cela n'a aucune importance.
Essayer plusieurs fois les commandes
p = 0.5;
U = rand();
if ( U < p )
disp("Pile");
else
disp("Face");
end
[Editor] de la fenêtre de base de Scilab)
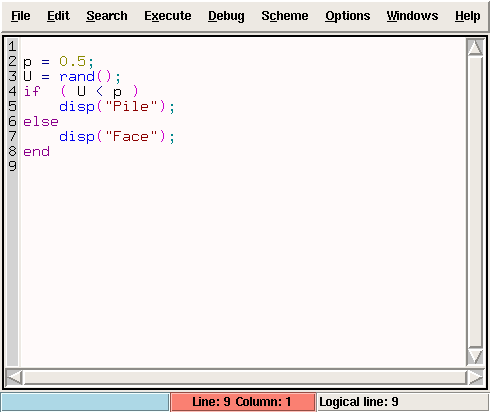
puis de les exécuter en cliquant le Menu
[Execute] puis [Load into Scilab] ou en tapant
<Ctrl-L> autant de fois que l'on veut exécuter le programme,
le résultat s'affichant dans la fenêtre de base.
Probabilité uniforme
--> K = 10; ceil(K*rand()), ceil(K*rand()), ceil(K*rand())
pour simuler des tirages dans l'espace Ω = {1,...,K}
muni de la probabilité uniforme.
Remplacer ceil par floor pour tirer dans
Ω = {0,...,K-1}
--> aleas = floor(8*rand(3,5))
pour une matrice 3x5 d'entiers aléatoires de probabilité uniforme
dans {0,..,7}.
Histogrammes
Pour contrôler visuellement si des "données" (ou des simulations)
suivent une loi déterminée, on peut en tracer un histogramme.
C'est un diagramme en "boites", basées en abscisse par les intervalles
consécutifs d'une subdivision et dont les surfaces sont
égales aux fréquences de "données" ("data")
tombant dans l'intervalle de base.
La fonction histplot(s, data) permet de tracer un histogramme,
elle prend deux arguments :
s, la subdivision, qui doit être un vecteur
(ligne ou colonne)
strictement croissant de K+1 piquets
s(1) < s(2) < ... < s(K+1)
encadrant K intervalles adjacents
Ik = ]s(k),s(k+1)] ;
data qui est un vecteur de données
ou de tirages aléatoires.
K rectangles (ou "boites") de l'histogramme, sa
surface est égale à la proportion de data qui tombent dans
sa largeur Ik.
Si toutes les données sont comprises entre les bornes extrêmes s(1)
et s(K+1), la surface totale de l'histogramme est égale à 1.
histplot fait deux choses :
fN(Ik) = Nk/N :
le nombre Nk de valeurs de data qui sont
dans Ik divisé par le nombre total
N = length(data)
et
Ik et de
surface fN(Ik) (en noir par défaut).
k dans 1:K.
Histogrammes pour des valeurs entières
Lorsque les valeurs des données appartiennent à un intervalle d'entiers
F = a:b, il faut adapter la subdivision s pour que ses
piquets encadrent régulièrement chacun des entiers de
F par des demi-entiers.
Le mieux est de poser s = a-0.5:b+0.5 en procédant, par exemple,
comme suit
--> K = 8, F = 1:K, s = 0.5:K+0.5
Pour chaque entier k ∈ F, les intervalles
Ik = ]k-0.5,k+0.5]
de la subdivision s sont tous de longueur 1 :
la hauteur de chacune des boites sera égale à sa surface.
Par exemple, soit un vecteur data de N (= 1000) tirages
aléatoires de probabilité uniforme sur l'intervalle d'entiers F
--> N = 1000, data = ceil(K*rand(1, N) );
on trace son histogramme en noir et la probabilité uniforme sur
F en bâtons bleus
--> clf, histplot(s, data), plot2d3(F, ones(F)/K, 2)
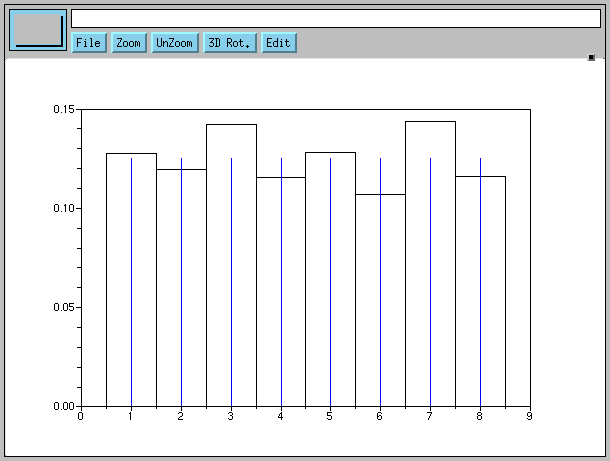
Pour chaque entier k ∈ F, la hauteur du rectangle de base
Ik est égale à la fréquence Nk/N :
le nombre de fois Nk où la valeur k apparait dans
data divisé par le nombre total de tirages N.
On compare avec le graphe en bâtons (plot2d3) de la probabilité
théorique (ici, la constante 1/K), qui, à chaque fois, doit être
approchée par la fréquence correspondante (on verra dans la suite du
cours que cette propriété fondamentale est une conséquence de la
fameuse Loi des Grands Nombres).
Remarquer l'utilisation de ones(F)/K pour obtenir un vecteur constant
de même taille que F (c'est le fameux truc qu'on trouvait un peu vicieux
mais qui, finalement, est bien commode).
Les noms de programmes Scilab se terminent par l'extension .sci
ou .sce
Simulations et histogramme de loi binomiale
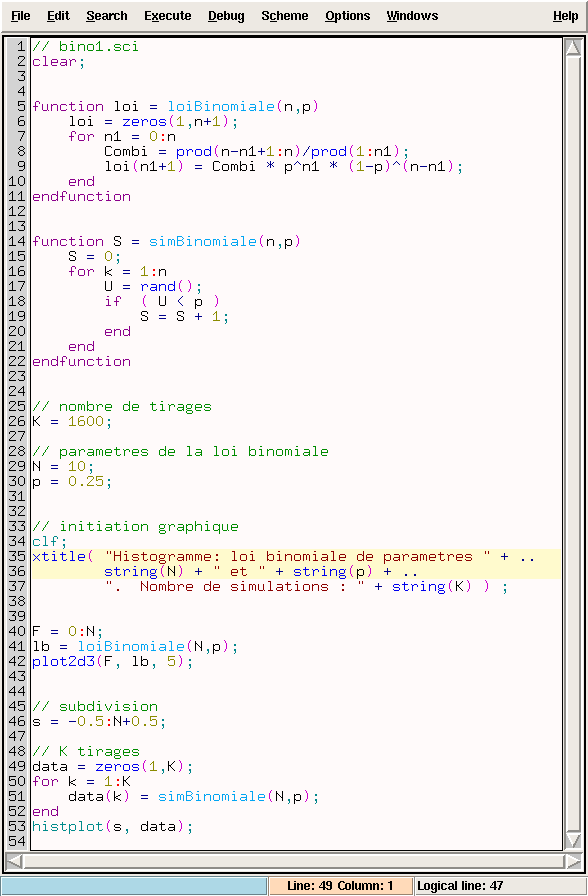
Charger le programme [bino1.sci] dans l'éditeur de texte de Scilab
pour pouvoir le lire et le modifier à votre guise. Le sauvegarder
(touches <Ctrl-S>) et l'exécuter
(touches <Ctrl-L>).
Ce programme simule K = 1600 tirages successifs d'entiers aléatoires
de loi binomiale de paramètres N = 10 et p = 0.25,
puis il en trace l'histogramme en noir qui est comparé à la loi en rouge.
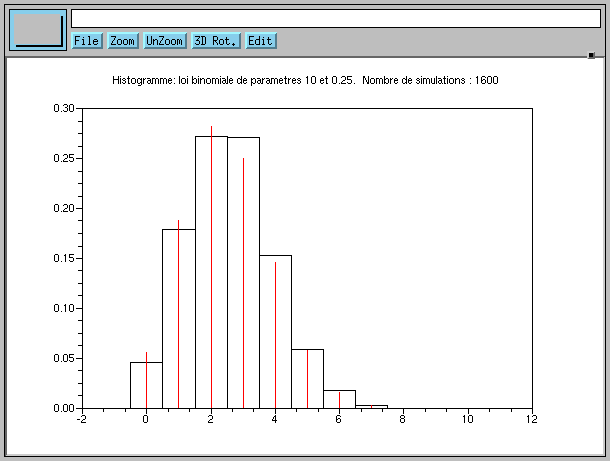
On observe que les fréquences (l'histogramme en noir) sont bien voisines des probabilités (en rouge), ce qui valide le procédé de simulation employé.
En ce qui concerne la rédaction d'un programme, deux grands principes
point-virgule (;), cela évitera les affichages
intempestifs dans la fenêtre de base lors de l'exécution et
d'avoir à y répondre (en anglais) à [More (y or n ) ?].
Les commentaires sont précédés de //
sur la même ligne,
// bino1.sci
est le nom du programme.
Ensuite vient une précaution
clear;
elle efface toutes les variables (et les fonctions de
l'utilisateur) précédentes, cela élimine des occasions
de bugs difficilement détectables, d'autant que les messages
d'erreurs de Scilab peuvent être obscurs !
Puis deux fonctions sont définies.
La fonction loiBinomiale prend comme arguments les paramètres
n et p de la loi binomiale et en renvoie le vecteur
ligne loi de dimension n+1
de ses probabilités :
function loi = loiBinomiale(n,p)
loi = zeros(1,n+1);
for n1 = 0:n
Combi = prod(n-n1+1:n)/prod(1:n1);
loi(n1+1) = Combi * p^n1 * (1-p)^(n-n1);
end
endfunction
function valeur_de_retour =
nom_de_fonction(arguments,...)
et se termine par
endfunction
Entre ces deux lignes, le bloc de code Scilab est
indenté de 4 espaces.
La valeur_de_retour est une variable de la fonction,
elle doit y être définie et, au final, valoir - justement -
la valeur de retour !
Dans le cas présent, par souci d'efficacité, elle est initialisée
comme un vecteur nul de la bonne taille : ce n'est pas obligatoire,
mais on aura avantage à procéder ainsi pour toute matrice
utilisée.
Remarquer la syntaxe de la boucle for dont l'indice de comptage
n1 parcourt la progression arithmétique 0:n.
La boucle se termine par end, et le bloc entre
ces deux lignes (for ... et end) est aussi
indenté.
Bien entendu la variable Combi est le nombre de combinaisons de
n objets pris n1 à n1.
Le décalage d'indice n1+1 est dû au fait que les indices du
vecteur loi commencent à 1 (c'est agaçant, mais on a
déjà dit qu'il fallait faire avec !).
On peut simuler un tirage de loi binomiale de paramètres
n et p en comptant le nombre de fois où un événement de
probabilité p est réalisé (succès) parmi n
essais :
function S = simBinomiale(n,p)
S = 0;
for k = 1:n
U = rand();
if ( U < p )
S = S + 1;
end
end
endfunction
{U < p} se produit avec la probabilité p
on a alors S = S + 1 (sinon S = S + 0), c'est le nombre de
succès.
Le bloc if (le else est facultatif) se termine aussi par
end.
On remarque l'absence de then, en effet, il pose des problèmes
lorsqu'il est mal placé ; ne pas le mettre, mais passer à la
ligne (et indenter) après la condition qui ici est mise entre
parenthèses.
Puis on initialise les paramètres du programme, nombre de tirages...
Ils peuvent être modifiés ici.
// nombre de tirages
K = 1600;
// parametres de la loi binomiale
N = 10;
p = 0.25;
clf;
xtitle( "Histogramme: loi binomiale de parametres " + ..
string(N) + " et " + string(p) + ..
". Nombre de simulations : " + string(K) ) ;
guillemets ("),
se concatènent par l'opérateur + .
Les scalaires sont convertis en chaînes par la fonction string.
On place deux points succesifs (..) avant le passage
à ligne lorsque l'on coupe une instruction.
On calcule et on trace en bâtons rouges la loi binomiale
F = 0:N;
lb = loiBinomiale(N,p);
plot2d3(F, lb, 5);
K simulations dans le vecteur data et
on en dessine l'histogramme
(le logiciel faisant le calcul des fréquences et leur dessin
par la fonction histplot)
// subdivision
s = -0.5:N+0.5;
// K tirages
data = zeros(1,K);
for k = 1:K
data(k) = simBinomiale(N,p);
end
histplot(s, data);
Simulations et histogramme de loi exponentielle
[expo.sce]
Ce programme fait N = 1600 tirages successifs d'une variable
aléatoire (v.a.) de loi exponentielle de paramètre
lambda = 1, il en trace l'histogramme en noir qui est comparé
à la densité en rouge.
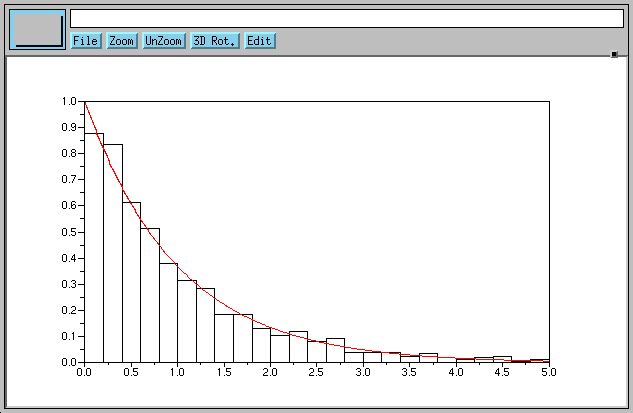
Comme en C/C++ et en Java les commentaires sont précédés
de // sur la même ligne,
// expo.sce
est le nom du programme.
Ensuite viennent deux précautions
clear;
rand("uniform");
La première efface toutes les variables (et les fonctions de
l'utilisateur) précédentes, cela élimine des occasions
de bugs difficilement détectables, d'autant que les messages
d'erreurs de Scilab sont particulièrement abscons !
La seconde bascule le générateur de nombres aléatoires de Scilab
en mode uniforme (qui est d'ailleurs le mode par défaut).
Puis on initalise les paramètres du programme, c'est ici, et seulement ici,
qu'il faut intervenir pour les modifier
lambda = 1;
N = 1600;
a = 0;
b = 5;
[a,b] correspond à la base de la fenêtre graphique.
Deux fonctions sont définies
function y = densExpo(para, x)
if ( x < 0 )
y = 0;
else
y = para*exp(-para*x);
end
endfunction
function X = simuExpo(para)
U = rand();
X = -log(U)/para;
endfunction
Tous les blocs, en particulier if (else), se terminent par
end.
On remarque l'absence de then, en effet, il pose des probèmes
lorsqu'il est mal placé ; ne pas le mettre, mais passer à la
ligne après la condition (qui ici est mise entre parenthèses).
Voici le corps du programme, on commence par procéder aux N
tirages avec une boucle qui remplit le vecteur data
s = linspace(a, b, 21);
data = zeros(1,N);
for n = 1:N
data(n) = simuExpo(lambda);
end
s sera utilisée pour l'histogramme.
Il est plus efficace, en Scilab, d'initialiser un vecteur à sa taille
avant usage, ce qui est fait pour data par la fonction zeros.
Puis, on calcule la densité
x = linspace(a, b, 501);
px = zeros(x);
for i = 1:length(x)
px(i) = densExpo(lambda, x(i));
end
px est initialisé et on en profite pour
s'assurer qu'il est de même taille que x.
Remarquer que, s'ils n'ont pas la même dimension, les vecteurs s et
x ont les mêmes extrémités (a et b).
Et, enfin, le graphisme
clf;
xtitle( "Histogramme: loi exponentielle de parametre " + ..
string(lambda) + ". Nombre de simulations : " + ..
string( N) ) ;
histplot(s, data);
plot2d(x, px, 5);
Autres versions
[expo2.sce]
[bino2.sci]